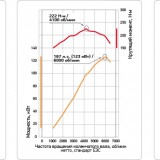
Что такое Уравнения движения летательного аппарата?
Уравнения движения летательного аппарата
Уравнения движения летательного аппарата
Обычно при анализе движения ЛА его рассматривают как абсолютно жёсткое тело. В этом случае в У. д. можно выделить две группы уравнений: У. д. центра масс (ЦМ) и У. д. относительно ЦМ. Если пренебречь вращением Земли, У. д. ЦМ ЛА можно представить в виде:

где m — масса ЛА, Vi (i = х, у, z), (Ω)i, gi, Ri — проекции векторов скорости V ЛА и его угловой скорости (Ω) в выбранной системе координат (СК), ускорения свободного падения g действующей на ЛА активной силы R, включающей аэродинамическую. силу RA (см. Аэродинамические силы и моменты) и тягу Р двигательной установки, на оси координат. Выбор СК зависит от решаемой задачи. Часто используется траекторная СК; в этом случае
(), () = () = 0.
Если пренебречь кривизной земной поверхности, что допустимо при скоростях полёта, значительно меньших первой космической, то

где (ψ)а — скоростной угол рыскания, (Θ) — угол наклона траектории, и У. д. ЦМ принимают вид:

где (φ) — угол заклинения тяги (угол между направлением тяги и продольной осью ЛА), (α) — угол атаки, (β) — угол скольжения, (γ)a — скоростной угол крена, Ха, Yа, Zа — аэродинамическое сопротивление, подъёмная и боковая силы. Приведённая система уравнений дополняется кинематическими соотношениями, определяющими положение ЦМ ЛА, которые в рассматриваемом случае имеют вид:

(здесь Н — высота полёта, Х и Z — продольная и боковая дальности).
Вторая группа У. д. имеет наиболее простой вид в связанной СК, оси которой направлены по главным осям инерции ЛА:

где (ω)x, y, z — соответственно скорости крена, рыскания и тангажа, Мх, у, z — проекции вектора полного момента М действующих на ЛА сил (аэродинамические и тяги) на соответствующие оси СК, Iх, y, z — главные моменты инерции ЛА. Эта система уравнений дополняется кинематическими соотношениями, определяющими изменения углов тангажа, рыскания и крена (соответственно (), (ψ) и (γ)):

• При отсутствии ветровых возмущений углы (α), (β) и (γ)a определяются с помощью равенств:
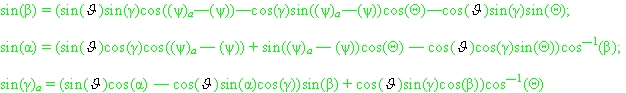
(подразумевается, что углы (γ) и (γ)a отсчитываются от одного и того же направления). Приведённые уравнения при необходимости дополняются уравнениями, определяющими изменения массы и моменты инерции ЛА вследствие выгорания топлива.
Входящие в уравнения аэродинамические силы и моменты, тяга двигательной установки являются функциями высоты и скорости полёта, угловых скоростей, углов атаки и скольжения и др. параметров. Задавшись конкретными выражениями для этих функций, можно замкнуть систему У. д. и проинтегрировать её. См. также Боковое движение, Продольное движение.
Авиация: Энциклопедия. — М.: Большая Российская Энциклопедия.
Главный редактор Г.П. Свищев.
1994.
.